相机模型以及FOV计算
一、相机模型
相机将三维世界中的坐标点(单位为米)映射到二维图像平面(单位为像素)的过程 能够用一个几何模型进行描述。这里介绍一下常用的相机模型——针孔相机模型。
1.针孔相机模型
针孔相机模型可以理解为通过小孔呈像原理将三维世界中的景象投射到二维成像平面上。如下图所示:

这里O−x−y−z为相机坐标系,一般Z轴向前,X轴向右,Y轴向下,O为相机的光心,同时也是针孔模型中的针孔,现实世界的空间点P经过小孔O投影之后,落在物理成像平面O′−x′−y′上,成像点P′,设P的坐标为[X,Y,Z]T,P′为[X′,Y′,Z′]T,物理成像的平面到相机光心(小孔)的距离为f(焦距)。如上图右侧所示,根据三角形的相似关系有:
fZ=−X′X=−Y′Y
其中负号表示成的像是倒立的。为了简化模型,我们把可以成像平面对称到相机前方,和三维空间点一起放在摄像机坐标系的同一侧,这样可以去掉负号,同时大多数相机输出的图像并不是倒像——相机自身 的软件会帮你翻转这张图像,所以你看到的一般是正着的像,也就是对称的成像平面上的像。由于输出的图像已经做了预处理,所以理解成在对称平面上的像,并不会带来什么坏处。可以参考下图:

整理可以得到:
X′Y′=fZX=fZY
2.像素坐标系
上面描述了空间中点P和它的像之间的空间关系,但是我们最终获得的是一个个的像素,这需要在成像平面上对呈的像进行采样和量化,将光线转换为图像的像素。设在物理成像平面上固定着一个像素平面O−u−v。我们在像素平面得到了P′的像素坐标:[u,v]T。像素坐标系为下图所示:

原点O′ 位于图像的左上角,u轴向右与x轴平行,v轴向下与y轴平行。像素坐标系与成像平面之间,相差了一个缩放和一个原点的平移。我们设像素坐标在u轴上缩放了α倍,在v上缩放了β倍。同时,原点平移了[cx,cy]T。那么,P′的坐标与像素坐标$ \begin{bmatrix}u ,& v \end{bmatrix}^{T}$的关系为:
{u=αX′+cxv=βY′+cy
将此式与之前的式子进行合并:
{u=αX′+cxv=βY′+cy
X′Y′=fZX=fZY
同时令αf合并成fx,βf合并成fy,其中f的单位是米,α,β的单位为像素每米,合并得到的fx,fy的单位为像素,得到:
{uv=αfZX+cx=βfZY+cy=fxZX+cx=fyZY+cy
将该式写成矩阵形式,
⎣⎢⎡uv1⎦⎥⎤=Z1⎣⎢⎡fx000fy0cxcy1⎦⎥⎤⎣⎢⎡XYZ⎦⎥⎤=Z1KP
按照习惯将Z移到左侧:
Z⎣⎢⎡uv1⎦⎥⎤=⎣⎢⎡fx000fy0cxcy1⎦⎥⎤⎣⎢⎡XYZ⎦⎥⎤=KP
将⎣⎢⎡fx000fy0cxcy1⎦⎥⎤作为相机的内参矩阵K,内参可以利用棋盘网格或者apriltag码方式进行标定。内参一般是不会变化的,除非焦距等参数发生了改变。
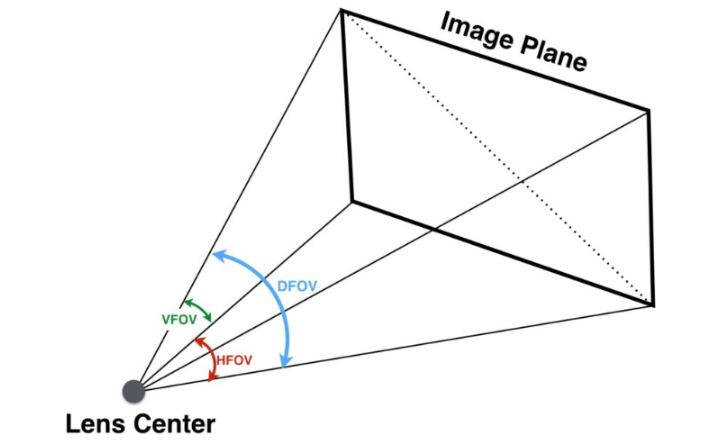
二、FOV相关计算公式
1.FOV简介
FOV的全称是Field of View (视场角),它表示相机或者人眼可以接收或者显示的影像的角度范围。由于相机的成像原理,一般都会有视场角的限制。如下图所示当相机的CCD或CMOS传感器的成像平面W一定时,FOV由焦距f决定,当焦距越大时,看的越远 但是FOV就会越小。当焦距越小时,FOV会变大,但是看到的范围就会变近。

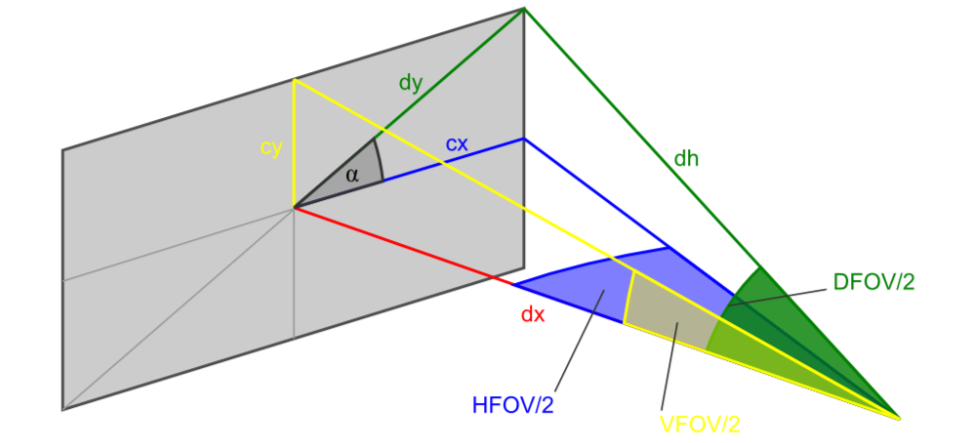
2.FOV相关的计算公式
主要分为水平FOV,垂直FOV和对角FOV。其中水平FOV由焦距和sensor的宽度W决定,垂直FOV由焦距和sensor的高度H决定,DFOV由焦距和sensor的宽度W和高度H决定。


相关的计算公式如下,其中fx,cx,fy,cy为相机去畸变后的内参:
水平方向:HFOV=FOVhorizontal=2∗arctan(fxcx)=2∗arctan[tan(2DFOV)cos(arctan(cxcy)]垂直方向:VHOF=FOVvertical=2∗arctan(fycy)=2∗arctan[tan(2DFOV)sin(arctan(cxcy)]
参考链接
相机的FOV计算公式_renmengqisheng的博客-CSDN博客
VR、AR、XR设计中的图像尺寸关系 - 知乎 (zhihu.com)